Aenean ornare velit lacus, ac varius enim lorem ullamcorper dolore aliquam.
What is divergence?
Divergence is a static stability problem. Unlike structural analysis where the action of a load results in a one-single deformation, in aeroelasticity the action of a load creates a deformation which in turn changes the load. This change in load will then try to change the deformation which then again changes the load acting on the wing and so on. It could therefore lead to a case where the load keeps increasing with the change in deformations leading to a structural failure.
Divergence is a failure that results due to torsional deformation of the wing and therefore is also called Torsional Divergence. Here, with an aerodynamic force (Lift), the flexible angle of attack changes, which also changes the aerodynamic forces acting on the wing. This could then keep increasing the flexible angle of attack until a point where the wing breaks. Let us analyze divergence through a typical section, followed by looking into the concepts of a swept wing.
$$M_{\text{equilibrium}} = M_{AC} + \text{Lift} \cdot (0.5 + a) \cdot b - K_\theta \cdot \theta = 0$$
where,
$$M_{AC} = q \cdot S \cdot (C_{M_{AC_\beta}} \cdot \beta \cdot (2b) + C_{M_{AC}} \cdot (2b))$$ $$\text{Lift} = q \cdot S \cdot C_{L_\alpha} \cdot (\alpha_0 + \theta)$$
$$\theta = \frac{M_{AC} + q \cdot S \cdot C_{L_\alpha} \cdot \alpha_0 \cdot (0.5 + a) \cdot b}{K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b}$$
For divergence to occur, the value of theta must become infinity i.e., the denominator becomes zero. Finding the pressure that corresponds to this would give us the divergence pressure.
$$K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b = 0$$ $$q_{\text{divergence}} = \frac{K_\theta}{S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b}$$However, it is not clear from this analysis whether the divergence pressure must be greater than this value or lesser than this value. To find this out there are two approaches. 1. Use \( \frac{\partial M_{\text{equilibrium}}}{\partial\theta} < 0 \) or 2. use the eigenvector analysis. Let us use the eigenvector approach.
For stability, we know that \( K_\theta X = K_{\text{aerodynamic}} X \)
$$\begin{pmatrix} K_h & 0\\ 0 & K_\theta \end{pmatrix} \begin{pmatrix} h\\ \theta \end{pmatrix} = \begin{pmatrix} 0 & -q \cdot S \cdot C_{L_\alpha}\\ 0 & q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b \end{pmatrix} \begin{pmatrix} h\\ \theta \end{pmatrix}$$ $$\begin{pmatrix} K_h & q \cdot S \cdot C_{L_\alpha}\\ 0 & K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b \end{pmatrix} \begin{pmatrix} h\\ \theta \end{pmatrix} = 0 $$The matrix above must be positive definite to be stable. With the help of the eigenvalues, and equating the determinant to zero, we get:
$$\begin{pmatrix} K_h - \lambda_1 & q \cdot S \cdot C_{L_\alpha}\\ 0 & K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b - \lambda_2 \end{pmatrix} = 0 $$We know the determinant of a matrix is equal to the product of the eigenvalues. Here it is $\lambda_1 \cdot \lambda_2$
$$\lambda_1 = K_h,$$which is always positive as it is the stiffness
$$\lambda_2 = K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b$$should also be positive to make the determinant positive. Hence,
$$K_\theta - q \cdot S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b > 0$$ $$q_{\text{divergence}} < \frac{K_\theta}{S \cdot C_{L_\alpha} \cdot (0.5 + a) \cdot b}$$Divergence analysis for a semi-rigid wing
In the context of divergence, adding a sweep angle (backward sweep) would help in reducing divergence. Let us explore a backward-swept wing as shown in Figure 1. First, some terminologies that will be used will be defined.
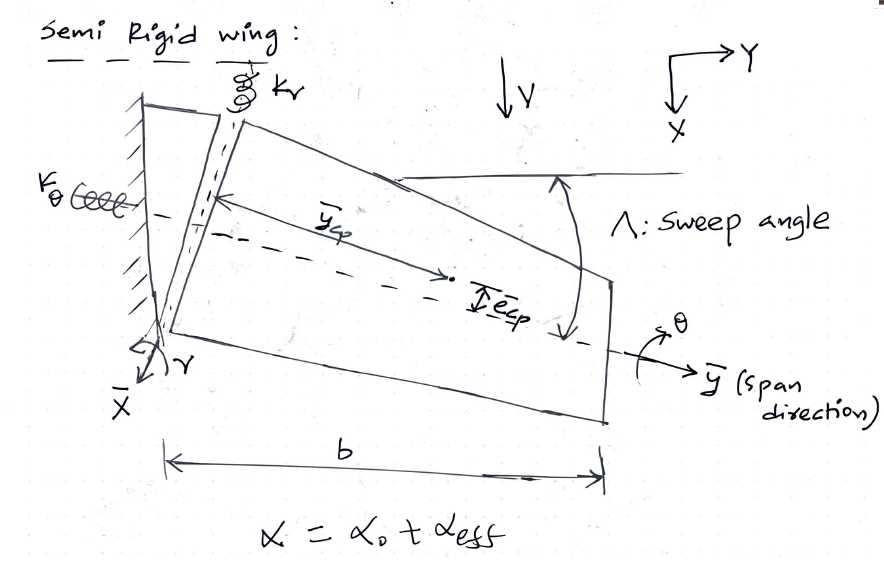
\(y:\) is the axis perpendicular to the velocity along which the flexible angle of attack changes. (always perpendicular to the flow velocity).
\(\overline{x}:\) is the axis perpendicular to the span direction and the degree of freedom (twist) is \(\gamma\).
\(K_\gamma:\) is the stiffness of the wing along the \(\gamma\) degree of freedom.
\(K_\theta:\) is the stiffness of the wing along the \(\theta\) degree of freedom.
\(\overline{y}:\) is the axis along the span direction and the degree of freedom (twist) is \(\theta\).
\(\overline{y_{cp}}\): is the distance of the center of pressure from the \(\overline{x}:\) axis.
\(\overline{e_{cp}}\): is the distance of the center of pressure from the \(\overline{y}:\) axis.
\(\Lambda:\) is the sweep angle.
\(\alpha_0:\) is the rigid angle of attack.
\(\alpha_{eff}:\) Flexible angle of attack.
Resolving we get,
$$\alpha_{eff} = \theta * \cos \Lambda - \gamma * \sin \Lambda$$
Writing the equation for stability gives:
$$\begin{pmatrix}
K_\gamma & 0\\
0 & K_\theta
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix} = \begin{pmatrix}
L * \overline{y_{cp}}\\
L * \overline{e_{cp}}
\end{pmatrix} $$
$$\begin{pmatrix}
K_\gamma & 0\\
0 & K_\theta
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix} = \begin{pmatrix}
q*S*C_{L_\alpha} *\alpha_{eff}* \overline{y_{cp}}\\
q*S*C_{L_\alpha} *\alpha_{eff} * \overline{e_{cp}}
\end{pmatrix} $$
Substituting, \(\alpha_{eff} \) in terms of \(\theta\) and \(\gamma\) as resolved earlier gives:
$$\begin{pmatrix}
K_\gamma & 0\\
0 & K_\theta
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix} = S*C_{L_\alpha} * \begin{pmatrix}
-q * \overline{y_{cp}} * \sin \gamma & q * \overline{y_{cp}} * \cos \gamma\\
-q * \overline{e_{cp}} * \sin \gamma & q * \overline{e_{cp}} * \cos \gamma
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix}$$
$$\begin{pmatrix}
K_\gamma & 0\\
0 & K_\theta
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix} = S*C_{L_\alpha} * \overline{y_{cp}} * \cos \gamma * \begin{pmatrix}
-q * \tan \gamma & q \\
-q * \widetilde{e} * \tan \gamma & q * \widetilde{e}
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix}$$
Substituting, \(\widetilde{e} = \frac{\overline{e_{cp}}}{\overline{y_{cp}}} \), \(\widetilde{K_\gamma} = \frac{K_\gamma}{ S*C_{L_\alpha}*\cos \gamma}\), and \(\widetilde{K_\theta} = \frac{K_\theta}{ S*C_{L_\alpha}*\cos \gamma}\)
$$\begin{pmatrix}
\widetilde{K_\gamma} + q*\tan\gamma & -q\\
q*\widetilde{e}*\tan\gamma & \widetilde{K_\theta}-q*\widetilde{e}
\end{pmatrix} \begin{pmatrix}
\gamma\\
\theta
\end{pmatrix} = 0 $$
For a nontrivial solution, the matrix's determinant must be zero. Solving it for q we get:
$$q_{divergence} = \frac{\widetilde{K_\gamma}*\widetilde{K_\theta}}{\widetilde{K_\gamma}*\widetilde{e}-\widetilde{K_\theta}*\tan\gamma}$$
(Note: If the sweep angle is zero, we get the same condition as we obtained using the typical section.)
The above expression for divergence also signifies one more thing. If the denominator is zero, then the divergence pressure is infinity meaning divergence would never occur at any pressure. This angle is known as isoclinic angle and it is equal to:
$$\tan \gamma = \frac{\widetilde{K_\gamma}*\widetilde{e}}{\widetilde{K_\theta}}$$
References
- Swept wing image credits: Dr. Roeland De Breuker and TU Delft
- Equations explained here are mainly part of the course given by Dr. Roeland De Breuker at TU DELFT in the course Fundamentals of Aeroelasticity
- Thumbnail image credits: https://en.wikipedia.org/wiki/Aeroelasticity
