
Aenean ornare velit lacus, ac varius enim lorem ullamcorper dolore aliquam.
Ever had your vehicle run out of fuel far away from the gas station? Chances are you would have taken gasoline from your friend's vehicle using a thin tube, sucking on it to start the flow, and then magically filling the bottle with petrol using no other external force. If you owned an aquarium without a drain, chances are you would have emptied it using a pipe filled with water. If you regularly fill in detergent in your washing machine, you would have noticed a mark for the maximum level that the detergent can be filled up to. If you accidentally go over the limit, the detergent would drain itself out before you start the machine.
There are other practical examples in our daily life that specifically take advantage of the Siphons operating principle to achieve regular tasks. Irrigating fields with multiple channels can be achieved by digging and filling the water on one side and then laying pipes filled with water into each of these channels. If you own a swimming pool without a drain, you can empty it without expending any energy by just laying a pipe filled with water into the pool and connecting the other end to a lower level. A reservoir built near a hill can take advantage of this principle to supply water on the other side of the hill by laying a pipe over the hill.
Scientists are continuously working to prove/disprove that the blood circulation to a giraffe’s head is through the same principle. Siphons certainly appear to work like magic and everyone would have experienced the marvel of a siphon pipe at least once in their life. In this article, we go on to explain the principles of this amazing phenomenon and look into a special case of a siphon called the Pythagorean cup.

Though siphons are being used in a wide variety of applications from ancient times, the physics behind this phenomenon has been up for debate. The two most common theories explaining the operation of a siphon are: 1. using atmospheric pressure and gravity and 2. gravity and liquid cohesion. [1] Both models have their merits and limitations, and we will use the atmospheric pressure and gravity model to explain the working of a siphon in this article.
Let us apply the principles of fluid mechanics to understand why the liquid is being drained and what conditions need to be satisfied for a successful working of a siphon.
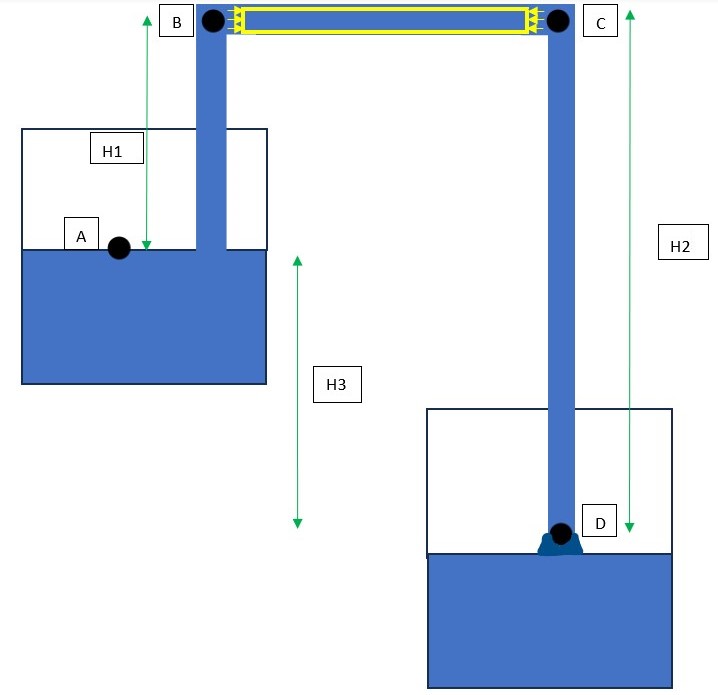
The above figure demonstrates a simple siphon connecting two vessels that are open to the atmosphere. This is an instance of a siphon taken to apply the principles of fluid statics to understand the initial behavior of how the liquid moves.
Points A is on the free surface of water in Vessel 1 and D is at the exit of the siphon in Vessel 2. Points C and D are at the top ends of the siphon. The points A and D are exposed to the atmosphere and the pressure here will be equivalent to the atmospheric pressure. From hydrostatic law, at points B and C, the pressure will be given by
PB = Patm − ρ*g*H1
PC = Patm − ρ*g*H2
As H1 < H2, PB must be greater than PC. If we write the equilibrium equation for the box(yellow) shown in the figure
Net Force, Fnet = PB * Area - PC * Area
This reveals a net positive force directed toward point C, which sustains the flow in the pipe. Once a part of the liquid moves, a new portion of the liquid takes its place due to pressure difference and this in turn maintains the flow till vessel one is emptied.
Now, let us consider the same setup while the fluid is in motion i.e., not an instance in time but a live setup where the liquid is being drained. Figure 2, shows this setup. Let us apply the Bernoulli principle between point A and point D to determine the velocity of the exit stream at D.
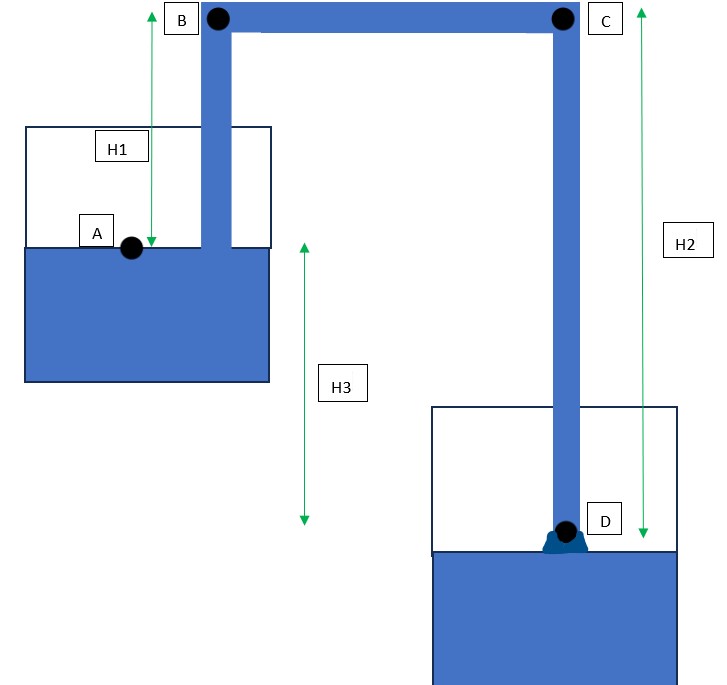
PA + 0.5 * ⍴ * VA2 + ⍴ * g * ZA = PD + 0.5 * ⍴ * VD2 + ⍴ * g * ZD
PA and PD are equal to the atmospheric pressure, VA is minimal due to the cross-section difference (can be derived from continuity equation, VA*AreaA = VD * AreaD), ZD can be taken as zero (datum) and then ZA will become equal to H3.
Therefore, ⍴ * g * H3 = 0.5 * ⍴ * VD2
VD = √ 2*g*H3
Note: Friction losses and minor losses in a pipe are not considered for simplicity. If they are accounted for, then H3 would effectively become H3 - Hlosses.
So, for a siphon to work, the following three conditions must be satisfied:
Let us now explore a special case of the siphon called the Pythagorean cup.
The Pythagorean cup, also known as the greedy siphon is one of the most fascinating examples involving the principles of fluid mechanics. The phenomenon allows the filling of the cup up to a certain height before draining the cup automatically. The story goes that Pythagoras used to give wine to his students in a special cup but only for a certain limit. Any student who gets greedy and fills the cup above a certain level will get all his wine drained automatically.
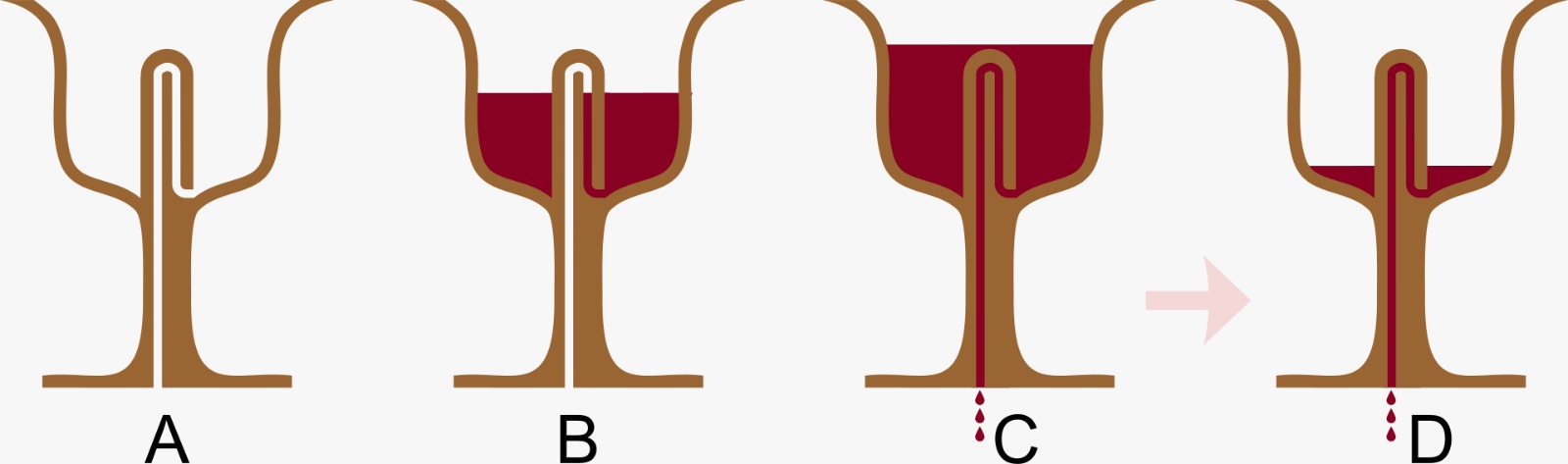
As shown in the image above, there are four distinct levels of the liquid. In Pic A, the cup is empty and as we begin to fill the cup, you will notice the level of the fluid rise (pic B). As the level rises, a notable observation is that when it surpasses the bend of the tube (pic C), the liquid initiates a self-draining process, depleting the cup almost entirely (pic D).
We have just discussed the principles on which a siphon works. The Pythagorean cup is a clever modification such that there is only one vessel that drains itself if a certain condition is achieved. We've established that the initial filling of the drain pipe is essential for initiating the flow, and this requirement is met when the liquid level surpasses the bend, filling the pipe through its own weight. Once gravity starts pulling on the fluid, the flow keeps happening due to pressure difference until almost all the fluid is drained.
The example mentioned regarding the detergent tray in a washing machine is a Pythagorean cup. If one fills the detergent above a certain level, it drains it automatically. In fact, this is how the machine drains the detergent into the machine once it starts running. It fills water into the detergent tray until the discharge from the tray is started.
Filling the Pythagorean cup beyond a certain level, regardless of the liquid, would cause it to drain. But filling it with two liquids, one much denser than the other, would make this phenomenon fail. Consider you pour a little mercury(more than the height of the bottom inlet) and the rest with water. As water is much less dense than mercury, the weight of water is not sufficient to push the mercury through the opening into the tube.